Paradoja de los gemelos

Paradoja de los gemelos. La paradoja de los gemelos (o paradoja de los relojes) es un experimento mental que analiza la distinta percepción del tiempo entre dos observadores con diferentes estados de movimiento.

Esta paradoja fue propuesta por Albert Einstein al desarrollar lo que hoy se conoce como la teoría de la relatividad especial. Dicha teoría postula que la medida del tiempo no es absoluta, y que, dados dos observadores, el tiempo medido entre dos eventos por estos observadores, en general, no coincide, sino que la diferente medida de tiempos depende del estado de movimiento relativo entre ellos. Así, en la teoría de la relatividad, las medidas de tiempo y espacio son relativas, y no absolutas, ya que dependen del estado de movimiento del observador. En ese contexto es en el que se plantea la paradoja.

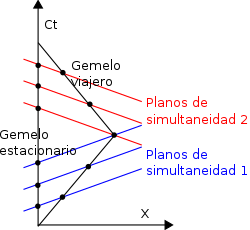
Paradoja de los gemelos Formulación de la paradoja

En la formulación más habitual de la paradoja, debida a Paul Langevin, se toma como protagonistas a dos gemelos (de ahí el nombre); el primero de ellos hace un largo viaje a una estrella en una nave espacial a velocidades cercanas a la velocidad de la luz; el otro gemelo se queda en la Tierra. A la vuelta, el gemelo viajero es más joven que el gemelo terrestre.

De acuerdo con la teoría especial de la relatividad, y según su predicción de la dilatación del tiempo, el gemelo que se queda en la Tierra envejecerá más que el gemelo que viaja por el espacio a gran velocidad (más adelante se prueba esto mediante cálculo) porque el tiempo propio del gemelo de la nave espacial va más lento que el tiempo del que permanece en la Tierra y, por tanto, el de la Tierra envejece más rápido que su hermano.

Pero la paradoja surge cuando se hace la siguiente observación: visto desde la perspectiva del gemelo que va dentro de la nave, el que se está alejando, en realidad, es el gemelo en la Tierra (de acuerdo con la Invariancia galileana) y, por tanto, cabría esperar que, de acuerdo con los cálculos de este gemelo, su hermano en la Tierra sería quien tendría que envejecer menos por moverse respecto de él a velocidades cercanas a la de la luz. Esto es, el gemelo de la nave es quien tendría que envejecer más rápido.

La paradoja quedaría dilucidada si se pudiese precisar quién envejece más rápido realmente y qué hay de erróneo en la suposición de que, de acuerdo con los cálculos del gemelo de la nave, es el gemelo terrestre quien envejece menos.

Paradoja de los gemelos Solución de la paradoja según la teoría de la relatividad especial

A Einstein le costó aclarar esta paradoja unos cuantos años, hasta que formuló la relatividad general y demostró que, ciertamente, es el gemelo de la Tierra quien envejece más rápido.

Sin embargo, aunque Einstein resolvió la paradoja en el contexto de la relatividad general, la paradoja puede resolverse dentro de los límites de la teoría de la relatividad especial, como muestra este artículo.

Para dilucidar la aparente paradoja es necesario realizar los cálculos desde el punto de vista del gemelo que permanece en la Tierra y desde el punto de vista del gemelo viajero, y ver que las estimaciones de tiempo transcurrido coinciden examinadas desde ambos puntos de vista.

El cálculo desde el punto de vista del gemelo terrestre es rutinario y muy sencillo. El cálculo desde el punto de vista del gemelo viajero es más complejo porque requiere realizar cálculos en un sistema no inercial. A continuación, se presentan las predicciones de la teoría aplicadas a ambos gemelos y se prueba que los resultados coinciden, demostrando que la aparente paradoja no es tal.

Paradoja de los gemelos Cálculo según el gemelo terrestre

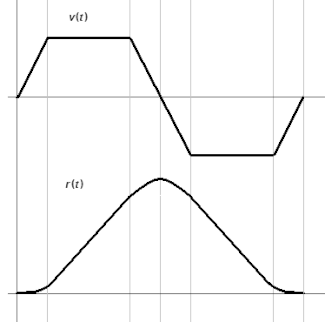
Las condiciones del experimento requieren que el gemelo viajero se aleje de la Tierra y más tarde regrese, lo cual necesariamente implica tener en consideración aceleraciones positivas y negativas. Simplificadamente, supondremos que el experimento puede llevarse a cabo en 5 etapas:

1. En el instante de tiempo t = 0 el gemelo viajero parte con «(pseudo)aceleración» (medida por el gemelo de la Tierra) w = F/m constante que lo aleja de ella. Se mueve aceleradamente entre los instantes medidos por el gemelo terrestre t = 0 y t = T₁, llegando a la velocidad V.
2. Cuando el gemelo viajero llega a una velocidad V apaga los motores de su nave, y sigue alejándose de la Tierra, ahora a velocidad constante. Durante esta etapa comprendida entre los instantes t = T₁ y t = T₁+T₂ el gemelo viajero se aleja de la Tierra a velocidad V.
3. Después de un tiempo viajando a velocidad uniforme el gemelo viajero pone en marcha los motores de su nave en sentido contrario y desacelera con la misma aceleración con la que aceleró, así transcurrido un tiempo de deceleración T₁ (medido por el gemelo en la Tierra) la velocidad será nula, y transcurrido otro intervalo T₁ la velocidad será –V (donde el signo negativo indica que la velocidad es en sentido contrario al que utilizó en su viaje de ida).
4. Una vez alcanzada la velocidad –V que hace que el gemelo viajero se aproxime a la Tierra de regreso con velocidad uniforme, el gemelo viajero permanece viajando aproximándose a la Tierra durante un intervalo de tiempo T₂.
5. Finalmente, para poderse reencontrar con su gemelo en la Tierra, el gemelo viajero desacelera, hasta llegar a la Tierra en reposo, eso requiere una aceleración igual a las anteriores aplicada durante un intervalo de tiempo T₁.

Por construcción la duración del viaje medido por el gemelo situado en la Tierra, es la suma de los tiempos de cada etapa, ya que hemos definido esas etapas a partir de lecturas del gemelo en la Tierra, para este gemelo la duración del viaje ha sido:

Ahora podemos comparar qué tiempo estima el gemelo de la Tierra que habrá medido su gemelo viajero. Para ello procedemos por etapas. En la primera etapa el tiempo que el gemelo de la Tierra estima ha transcurrido para el gemelo viajero, usando la relación entre la (pseudo)aceleración y la velocidad en un movimiento acelerado relativista, viene dado por:

Entre los instantes tiempo t = T₁ y t = T₁+T₂ (medidos por el gemelo terrestre) la nave espacial se mueve con velocidad uniforme V por tanto:

Juntando los resultados anteriores, en el momento del encuentro de acuerdo con los cálculos del gemelo terrestre, él y su gemelo viajero habrán notado tiempos diferentes de viaje dados por:

Es sencillo comprobar que para cualesquiera valores de w, T₁ y T₂, el segundo tiempo es siempre menor que el primero: , y por tanto, según el gemelo terrestre él mismo envejecerá más que el gemelo viajero.

Cálculo según el gemelo viajero

Los cálculos en el sistema de referencia no inercial del gemelo viajero son más complicados, aunque conducen exactamente al mismo resultado anterior. Todo ello sin necesidad de salirse del ámbito de la teoría de la relatividad especial. Para este cálculo introducimos las coordenadas asociadas al observador no inercial cuya relación con las coordenadas usadas por el gemelo terrestre es:

Durante la primera etapa del recorrido, el gemelo viajero está sometido a aceleración w. El tensor métrico, haciendo el cambio de coordenadas a las coordenadas asociadas a su sistema de referencia, es:

(2)

En este sistema de referencia el gemelo viajero está en reposo y el punto x = 0 se mueve según una geodésica:

(3){\displaystyle {\frac {d{\bar {u}}^{i}}{ds}}+{\bar {\Gamma }}_{ml}^{i}{\bar {u}}^{m}{\bar {u}}^{l}=0}

A partir de las componentes del tensor métrico dado por (2) el único símbolo de Christoffel que no se anula es {\displaystyle {\bar {\Gamma }}_{00}^{1}} y las ecuaciones de movimiento del gemelo terrestre visto por el gemelo viajero resultan ser:

(4){\displaystyle {\begin{cases}{\cfrac {d{\bar {u}}^{0}}{ds}}=0&{\mbox{con}}\quad {\bar {u}}^{1}={\cfrac {{\bar {u}}^{0}}{c}}{\cfrac {d{\bar {x}}}{d{\bar {t}}}}\\{\cfrac {d{\bar {u}}^{1}}{ds}}+{\bar {\Gamma }}_{00}^{1}{\bar {u}}^{0}{\bar {u}}^{0}=0&\Rightarrow \quad {\cfrac {d^{2}{\bar {x}}}{d{\bar {t}}^{2}}}+{\cfrac {w}{\left[1+{\frac {w^{2}{\bar {t}}^{2}}{c^{2}}}\right]^{\frac {3}{2}}}}=0\end{cases}}}

Integrando las ecuaciones de movimiento del gemelo terrestre observado por el gemelo viajero viene dado por:

(5){\displaystyle {\bar {x}}({\bar {t}})={\frac {c^{2}}{w}}\left[1-{\sqrt {1+{\frac {w^{2}{\bar {t}}^{2}}{c^{2}}}}}\right]}

Con esas expresiones el tiempo propio, estimado por el gemelo viajero, para la duración medida por él mismo y por su gemelo terrestre resultan ser idénticas a las calculadas por el gemelo terrestre:

(6a){\displaystyle T_{1}=\int d\tau =\int _{0}^{T_{1}}{\begin{matrix}\\\underbrace {\left[g_{00}+{\frac {2}{c}}g_{01}{\frac {d{\bar {x}}}{d{\bar {t}}}}-{\frac {1}{c^{2}}}\left({\frac {d{\bar {x}}}{d{\bar {t}}}}\right)^{2}\right]^{1/2}} _{=c}\end{matrix}}{\frac {d{\bar {t}}}{c}}}

(6b){\displaystyle {\bar {T}}_{1}=\int d{\bar {\tau }}=\int _{0}^{T_{1}}{\sqrt {g_{00}}}{\frac {d{\bar {t}}}{c}}=\int _{0}^{T_{1}}{\frac {d{\bar {t}}}{\sqrt {1+{\frac {w^{2}{\bar {t}}^{2}}{c^{2}}}}}}={\frac {c}{w}}\ln \left[{\frac {wT_{1}}{c}}+{\sqrt {1+{\frac {w^{2}T_{1}^{2}}{c^{2}}}}}\right]}

En la segunda etapa del viaje, el gemelo viajero pasa de nuevo a ser un observador inercial que se aleja con velocidad uniforme del gemelo terrestre. Sin embargo, aparece aquí un problema matemático con la elección de la métrica, y es que los requerimientos físicos implican que la métrica de un observador a lo largo de su trayectoria varía de manera continua sin saltos. Eso implica que debemos escoger coordenadas adecuadas para la segunda etapa del viaje, que garanticen la continuidad de la métrica percibida por el gemelo viajero, para que nuestros cálculos tengan sentido. Una posible elección de la métrica en ese caso viene dada por:¹

(7){\displaystyle g=-c^{2}{\sqrt {1-{\cfrac {V^{2}}{c^{2}}}}}d{\bar {t}}\otimes d{\bar {t}}-2Vd{\bar {t}}\otimes d{\bar {x}}+d{\bar {x}}\otimes d{\bar {x}}+d{\bar {y}}\otimes d{\bar {y}}+d{\bar {z}}\otimes d{\bar {z}}}

Finalmente para calcular la duración de la segunda etapa del viaje para ambos gemelos, pero haciendo los cálculos según el sistema de referencia del gemelo viajero, tenemos que seleccionar una forma de la métrica:

(7a){\displaystyle T_{2}=\int d\tau =\int _{T_{1}}^{T_{1}+T_{2}}{\begin{matrix}\\\underbrace {\left[g_{00}+{\frac {2}{c}}g_{01}{\frac {d{\bar {x}}}{d{\bar {t}}}}-{\frac {1}{c^{2}}}\left({\frac {d{\bar {x}}}{d{\bar {t}}}}\right)^{2}\right]^{1/2}} _{=c}\end{matrix}}{\frac {d{\bar {t}}}{c}}=(T_{1}+T_{2})-T_{1}}

(7b){\displaystyle {\bar {T}}_{2}=\int d{\bar {\tau }}=\int _{T_{1}}^{T_{1}+T_{2}}{\sqrt {g_{00}}}d{\bar {t}}=T_{2}{\sqrt {1-{\frac {V^{2}}{c^{2}}}}}={\frac {T_{2}}{\sqrt {1+{\frac {w^{2}T_{1}^{2}}{c^{2}}}}}}}

Estos resultados vuelven a coincidir con los cálculos que se hicieron desde el sistema inercial del gemelo terrestre. Como todas las cantidades vuelven a ser idénticas se cumple de nuevo que {\displaystyle T_{viaje}-{\bar {T}}_{viaje}>0}.

Esto aclara finalmente que:

1. Tanto según los cálculos y predicciones del sistema inercial del gemelo terrestre como los cálculos según el sistema no inercial del gemelo viajero, ambos concluirán que el gemelo terrestre es quien envejecerá más, ya que el tiempo medido durante el transcurso del viaje es mayor para él.
2. La paradoja puede ser resuelta dentro de la propia teoría de la relatividad especial, aunque se requiere el uso de sistemas inerciales y tener precauciones especiales para asegurar la continuidad de la métrica.

Resolución de la paradoja en relatividad general

Aunque la paradoja de los gemelos puede resolverse íntegramente dentro de la teoría especial de la relatividad, resulta interesante considerar el mismo problema desde el punto de vista de teoría de la relatividad general. Usando el enfoque de esa teoría más general, la parte del viaje en la que el gemelo viajero se mueve aceleradamente son percibidas por éste como si estuviera en el seno de un «campo gravitatorio efectivo» asociado a la aceleración, de acuerdo con lo postulado por el principio de equivalencia. Este punto de vista está bien representado en la solución que ofreció Einstein de la paradoja en 1918 dentro del marco de la teoría general.²

Según el enfoque de la relatividad general la diferencia acumulada de tiempo entre los dos gemelos puede ser explicada mediante una dilatación gravitacional del tiempo. De acuerdo con la relatividad general, la relación entre los tiempos propios acumulados por dos observadores situados en diferentes puntos de un campo gravitatorio estático puede representarse por:

Donde c es la velocidad de la luz y en la aproximación para campos gravitatorios débiles se puede identificar con el potencial gravitatorio clásico. Si ignoramos los efectos gravitatorios de la tierra y consideramos sólo los términos asociados a la aceleración del gemelo viajero podemos escribir la anterior ecuación como:

{\displaystyle \Delta \tau \approx \Delta {\bar {\tau }}\left(1-{\frac {\bar {\Phi }}{c^{2}}}\right)=\Delta {\bar {\tau }}\left(1-{\frac {a\ d}{c^{2}}}\right)}

Donde a es la aceleración y d es una distancia efectiva entre los dos gemelos.

Es importante notar que aunque la solución anterior se llame resolución según la relatividad general de hecho se realiza mediante observadores acelerados tal como fueron definidos por Einstein en 1907 en el contexto del principio de equivalencia y por tanto básicamente es equivalente a la solución de la teoría de la relatividad especial. De hecho, recientemente se ha probado que la solución de la relatividad general para campos gravitatorios homogéneos y estáticos y la solución de la teoría de la relatividad especial para aceleraciones finitas llevan a resultados idénticos.

Paradoja de los gemelos Evidencia experimental

Contrariamente a la idea más extendida, la paradoja no es el hecho de que un gemelo envejezca más rápido que el otro, sino en el razonamiento capcioso que sugería que los dos gemelos concluyen que es el otro quien envejecería más. Como se ha visto los cálculos de los dos gemelos concuerdan en que será el gemelo terrestre quien envejecerá más.

El hecho de que el tiempo transcurra de diferentes maneras para diferentes observadores, y que dos observadores puedan reencontrarse de nuevo en el mismo punto del espacio-tiempo habiendo envejecido uno menos que otro no constituye ninguna paradoja en teoría de la relatividad, sino que de hecho se trata de un hecho probado.

El experimento más claro que mostró el efecto de dilatación temporal no se llevó a cabo con un par de gemelos tal como hemos descrito sino con dos relojes idénticos. En 1971, J. C. Hafele y R. Keating, subieron varios relojes atómicos de cesio a bordo de aviones comerciales durante más de 40 horas y se comparó la lectura de estos con otro idéntico en Tierra sincronizado con el primero. El avión despegó e hizo un largo viaje, y aterrizó en el mismo punto de salida. Al comparar los dos relojes atómicos después del viaje, el del avión y el de la Tierra, ya no estaban sincronizados. El reloj atómico que había volado estaba ligeramente retrasado (muy ligeramente pero medible con dichos relojes, la diferencia de tiempos era de unas pocas centésimas de milésima de millonésima de segundo). Tras descontar ciertos efectos gravitatorios secundarios, y asumiendo que no hubo ningún error de medida, lo cual se comprobó controlando las condiciones y repitiendo el experimento varias veces, se concluyó que la única explicación posible venía por la teoría de la relatividad de Einstein. Los datos publicados por la revista Science en 1972 relativos al experimento de Hafele-Keating, difieren según la dirección de vuelo, y resultaron ser:

	nanosegundos ganados
	valor predicho por la teoría			valor medido
	efecto gravitacional (relatividad general)	efecto cinético (teoría de la relatividad especial)	total
Vuelo hacia el este	144±14	−184 ± 18	−40 ± 23	−59 ± 10
Vuelo hacia el oeste	179±18	96±10	275±21	273±7

Guardar

Guardar