Momento angular. El momento angular o momento cinético es una magnitud física de las tres mecánicas (mecánica clásica, cuántica y relativista). En el Sistema Internacional de Unidades el momento angular se mide en kg·m²/s. Esta magnitud desempeña respecto a las rotaciones un papel análogo al momento lineal en las traslaciones.
El nombre tradicional en español es momento cinético, pero por influencia del inglés angular momentum hoy son frecuentes momento angular y otras variantes como cantidad o ímpetu angular.
Bajo ciertas condiciones de simetría rotacional de los sistemas es una magnitud física que se mantiene constante con el tiempo a medida que el sistema va cambiando, lo cual da lugar a la llamada ley de conservación del momento angular. El momento angular para un cuerpo rígido que rota respecto a un eje es la resistencia que ofrece dicho cuerpo a la variación de la velocidad angular. Sin embargo, eso no implica que sea una magnitud exclusiva de las rotaciones; por ejemplo, el momento angular de una partícula que se mueve libremente con velocidad constante (en módulo y dirección) también se conserva
Momento angular en mecánica clásica
De una masa puntual
 es el producto vectorial de su momento lineal
es el producto vectorial de su momento lineal  por el vector
por el vector  .
.En mecánica newtoniana, el momento angular de una partícula o masa puntual con respecto a un punto O del espacio se define como el momento de su cantidad de movimiento 


El vector 


esto es, el producto del módulo del momento lineal por su brazo ( 
Momento angular y momento dinámico
Derivemos el momento angular con respecto al tiempo:
El primero de los paréntesis es cero ya que la derivada de 


donde 


Así, la derivada temporal del momento angular es igual al momento dinámico que actúa sobre la partícula. Hay que destacar que en esta expresión ambos momentos, 

Momento angular de un conjunto de partículas puntuales
El momento de un conjunto de partículas es la suma de los momentos angulares de cada una:
La variación temporal es:
El término de derecha es la suma de todos los momentos producidos por todas las fuerzas que actúan sobre las partículas. Una parte de esas fuerzas puede ser de origen externo al conjunto de partículas. Otra parte puede ser fuerzas entre partículas. Pero cada fuerza entre partículas tiene su reacción que es igual pero de dirección opuesta y colineal. Eso quiere decir que los momentos producidos por cada una de las fuerzas de un par acción-reacción son iguales y de signo contrario y que su suma se anula. Es decir, la suma de todos los momentos de origen interno es cero y no puede hacer cambiar el valor del momento angular del conjunto. Solo quedan los momentos externos:
El momento angular de un sistema de partículas se conserva en ausencia de momentos externos. Esta afirmación es válida para cualquier conjunto de partículas: desde núcleos atómicos hasta grupos de galaxias.
Momento de un sólido rígido
Tenemos que en un sistema inercial la ecuación de movimiento es:
Donde:
-
es la velocidad angular del sólido.
-
es el tensor de inercia del cuerpo.
Ahora bien, normalmente para un sólido rígido el tensor de inercia 
Donde 

Que resulta ser una ecuación no lineal en la velocidad angular.
Conservación del momento angular clásico
Cuando la suma de los momentos externos es cero 
Eso quiere decir que 

Consideremos un objeto que puede cambiar de forma. En una de esas formas, su Momento de inercia es 


En algunos casos el momento de inercia se puede considerar un escalar. Entonces la dirección del vector velocidad angular no cambiará. Solo cambiará la velocidad de rotación.
Hay muchos fenómenos en los cuales la conservación del momento angular tiene mucha importancia. Por ejemplo:
- En todos las artes y los deportes en los cuales se hacen vueltas, piruetas, etc. Por ejemplo, para hacer una pirueta, una bailarina o una patinadora toman impulso con los brazos y una pierna extendida para aumentar sus momentos de inercia alrededor de la vertical. Después, cerrando los brazos y la pierna, disminuyen sus momentos de inercia, lo cual aumenta la velocidad de rotación. Para terminar la pirueta, la extensión de los brazos y una pierna, permite disminuir la velocidad de rotación. Sucede lo mismo con el salto de plataforma o el trampolín. También es importante en el ciclismo y motociclismo, ya que la conservación del momento angular es la responsable de la sencillez con que es posible mantener el equilibrio.
- Para controlar la orientación angular de un satélite o sonda espacial. Como se puede considerar que los momentos externos son cero, el momento angular y luego, la orientación del satélite no cambian. Para cambiar esta orientación, un motor eléctrico hace girar un volante de inercia. Para conservar el momento angular, el satélite se pone a girar en el sentido opuesto. Una vez en la buena orientación, basta parar el volante de inercia, lo cual para el satélite. También se utiliza el volante de inercia para parar las pequeñas rotaciones provocadas por los pequeños momentos inevitables, como el producido por el viento solar.
- Algunas estrellas se contraen convirtiéndose en púlsar (estrella de neutrones). Su diámetro disminuye hasta unos kilómetros, su momento de inercia disminuye y su velocidad de rotación aumenta enormemente. Se han detectado púlsares con periodos rotación de tan sólo unos milisegundos.
- Debido a las mareas, la Luna ejerce un momento sobre la Tierra. Este disminuye el momento angular de la Tierra y, debido a la conservación del momento angular, el de la Luna aumenta. En consecuencia, la Luna aumenta su energía alejándose de la Tierra y disminuyendo su velocidad de rotación (pero aumentando su momento angular). La Luna se aleja y los días y los meses lunares se alargan.
Ejemplo
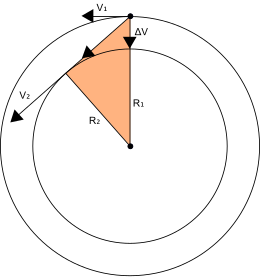
En el dibujo de la derecha tenemos una masa que gira, tenida por un hilo de masa despreciable que pasa por un tubito fino. Suponemos el conjunto sin rozamientos y no tenemos en cuenta la gravedad.
La fuerza que el hilo ejerce sobre la masa es radial y no puede ejercer un momento sobre la masa. Si tiramos del hilo, el radio de giro disminuirá. Como, en ausencia de momentos externos, el momento se conserva, la velocidad de rotación de la masa debe aumentar.
 a la masa. La nueva velocidad es la suma vectorial de la velocidad precedente y
a la masa. La nueva velocidad es la suma vectorial de la velocidad precedente y 
En el dibujo siguiente aparece la masa que gira con un radio 





o sea:
Y, si multiplicamos por la masa m {\displaystyle \scriptstyle {m}} 
Vemos como el momento angular se ha conservado: Para reducir el radio de giro hay que comunicar una velocidad radial, la cual aumenta la velocidad total de la masa.
También se puede hacer el experimento en el otro sentido. Si se suelta el hilo, la masa sigue la tangente de la trayectoria y su momento angular no cambia. A un cierto momento frenamos el hilo para que el radio sea constante de nuevo. El hecho de frenar el hilo, comunica una velocidad radial (hacia el centro) a la masa. Esta vez esta velocidad radial disminuye la velocidad total y solo queda la componente de la velocidad tangencial al hilo en la posición en la cual se lo frenó.
No es necesario hacer la experiencia dando un tirón. Se puede hacer de manera continua, ya que la fuerza que se hace recobrando y soltando hilo puede descomponerse en una sucesión de pequeños impulsos.
En mecánica relativista
En mecánica newtoniana el momento angular es un pseudovector o vector axial, por lo que en mecánica relativista debe ser tratado como el dual de Hodge de las componentes espaciales de un tensor antisimétrico. Una representación del momento angular en la teoría especial de la relatividad es por tanto como cuadritensor antisimétrico:
Puede verse que las 3 componentes espaciales forman el momento angular de la mecánica newtoniana L 

Momento angular en mecánica cuántica
En mecánica cuántica el momento angular es un conjunto de tres operadores para los cuales existe un conjunto de estados linealmente mente independientes 
Y que además satisfacen las siguientes relaciones de conmutación canónicas:
donde
-
es el símbolo de Levi-Civita y
-
Estas relaciones de conmutación garantizan que dichos operadores constituyen una representación del álgebra de Lie su(2) (que está relacionada, con el grupo recubridor universal del grupo de rotaciones tridimensional).
Por ejemplo el momento angular orbital 



Momento angular orbital
El momento angular orbital, tal como el que tiene un sistema de dos partículas que giran una alrededor de la otra, se puede transformar a un operador 
siendo r {\displaystyle \mathbf {r} } 
Usando coordenadas cartesianas las tres componentes del momento angular se expresan en el espacio de Hilbert usual para las funciones de onda, 
En cambio en coordenadas angulares esféricas el cuadrado y la componente Z se expresan como:
Los vectores propios o estados propios del momento angular orbital dependen de dos números cuánticos enteros 
Estos vectores propios expresados en términos de las coordenadas angulares esféricas son los llamados armónicos esféricos Yl, m(θ,φ), que se construyen a partir de los polinomios de Legendre:
Tienen especial importancia por ser la componente angular de los orbitales atómicos.
Conservación del momento angular cuántico
Es importante notar que si el hamiltoniano no depende de las variables angulares, como sucede por ejemplo en problemas con potencial de simetría esférica entonces todas las componentes del momento angular conmutan con el hamiltoniano:
y, como consecuencia, el cuadrado del momento angular también conmuta con el Hamiltoniano:
.
Y tenemos que el momento angular se conserva, eso significa que a lo largo de la evolución en el tiempo del sistema cuántico la distribución de probabilidad de los valores del momento angular no variará. Nótese sin embargo que como las componentes del momento angular no conmutan entre sí no se pueden definir simultáneamente. Sin embargo, si se pueden definir simultáneamente el cuadrado del momento angular y una de sus componentes (habitualmente se elige la componente Z). En particular si tenemos estados cuánticos de momento bien definido estos seguirán siendo estados cuánticos de momento bien definido con los mismos valores de los números cuánticos l y m.
En la cultura popular
En el episodio de Los Simpson How the Test was Won (‘Cómo se ganó la prueba’ en Hispanoamérica, y ‘La conquista del examen’ en España)», el director Seymour Skinner, aplica la conservación del momento angular para hacer girar un contenedor y rescatar a Ralph Wiggum de un barco lleno de desperdicios.











![{\frac {d{\mathbf {L}}}{dt}}={\frac {d}{dt}}\left[{\mathbf {I}}(t){\mathbf {\omega }}(t)\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/6bddd826dd817fbafde768bd3414368354eb0a1f)










![[{\hat {A}}_{i},{\hat {A}}_{j}]=i\hbar \epsilon _{{ijk}}{\hat {A}}_{k},\qquad \left[{\hat {A}}_{i},{\hat {{\mathbf {A}}}}^{2}\right]=0](https://wikimedia.org/api/rest_v1/media/math/render/svg/4eb3410f79a9ae6ceb7dec8152e209207a6e344a)



![\ {\hat {L}}^{2}=-\hbar ^{2}\left[{\frac {1}{\sin \theta }}{\frac {\partial }{\partial \theta }}\left(\sin \theta {\frac {\partial }{\partial \theta }}\right)+{\frac {1}{\sin ^{2}\theta }}{\frac {\partial ^{2}}{\partial \varphi ^{2}}}\right]\qquad {\hat {L}}_{z}=-i\hbar \left({\frac {\partial }{\partial \varphi }}\right)](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd30c86e05a7c83753069f358a53b0beffe65738)


![\left[{\hat {L}}_{i},H\right]=0](https://wikimedia.org/api/rest_v1/media/math/render/svg/b14bbb096767954e80cbd256138d04013279c30f)








