Potencia

Potencia. En física, la potencia (representada por el símbolo P) se dice que una fuerza realiza trabajo cuando altera el estado de movimiento de un cuerpo. El trabajo de la fuerza sobre ese cuerpo será equivalente a la energía necesaria para desplazarlo de manera acelerada. El trabajo es una magnitud física escalar que se representa con la letra 

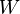
 (del inglés Works) y se expresa en unidades de energía, esto es en julios o Joules (J) en el Sistema Internacional de Unidades.

es una cantidad determinada de trabajo efectuado de alguna manera en una unidad de tiempo determinada. O sea, es la cantidad de trabajo por unidad de tiempo que algún objeto o sistema produce.

La potencia se mide en watts (W), unidad que rinde homenaje al inventor escocés James Watt y equivale a un julio (J) de trabajo realizado por segundo (s), es decir:

W = J/s

En el sistema anglosajón de medidas, esta unidad es reemplazada por los caballos de fuerza (hp).

La habilidad para comprender y medir la potencia con precisión fue un factor determinante en el desarrollo de los primeros motores a vapor, aparato sobre el cual se sostuvo la Revolución Industrial. En nuestros días, en cambio, suele estar asociada a la electricidad y a otro tipo de recursos energéticos modernos, pues también puede designar la cantidad de energía transmitida.

Tipos de potencia

Existen los siguientes tipos de potencia:

• Potencia mecánica. Aquella que se deriva de la aplicación de una fuerza sobre un sólido rígido, o bien un sólido deformable.
• Potencia eléctrica. En lugar de trabajo, se refiere a la cantidad de energía transmitida por unidad de tiempo en un sistema o circuito.
• Potencia calorífica. Se refiere a la cantidad de calor que un cuerpo libera al medio ambiente por unidad de tiempo.
• Potencia sonora. Se entiende como la cantidad de energía que una onda sonora transporta por unidad de tiempo a través de una superficie determinada.

Fórmulas de potencia

La potencia de una maquinaria nos indica si podrá realizar un trabajo.

La potencia se calcula, en términos generales, de acuerdo a la fórmula siguiente:

P = ΔE/ Δt

ΔE representa el cambio de energía o la variación de trabajo.

Δt representa el tiempo medido en segundos.

Sin embargo, cada tipo de potencia se expresa mediante su propia formulación, por ejemplo:

• Potencia mecánica. P(t) = F.v, aunque si existe una rotación del sólido y las fuerzas aplicadas alteran su velocidad angular, utilizaremos P(t) = F.v + M.ω en su lugar. F y M serán la fuerza resultante y el momento resultante, respectivamente; mientras que V y ω serán la velocidad del punto sobre el cual se calculó la resultante, y la velocidad angular del cuerpo.
• Potencia eléctrica. P(t) = I(t). V(t), donde I es la corriente circulando, medida en amperios, y V es la diferencia de potencial (la caída de voltaje) medida en voltios. En caso de que se trate de una resistencia en lugar de un conductor de electricidad, la fórmula a emplear será P = I²R = V²/R, donde R es la resistencia del material, medida en ohmios.
• Potencia calorífica. P = E/t, donde E es la energía calórica proporcionada, medida en julios (J). Nótese cómo ello es indiferente a los grados de calor.
• Potencia sonora. P_S = ʃI_s dS, donde I_s es la intensidad sonora y dS el elemento alcanzado por la onda.

W    =       F    .         Xtrabajo= fuerza . distanciacuando el trabajo es realizado por una fuerza oblicua ( o sea con una dirección o angulo determinado, la fórmula se transforma en:     W   =     F     .    X     .    cosθ trabajo= fuerza . distancia. cosθ

El concepto de trabajo, en Física, está íntimamente relacionado con las transformaciones que sufren los cuerpos. De entre todas ellas, una de las más evidentes y cómodas de estudiar es la de las transformaciones mecánicas (las transformaciones en el estado de movimiento de un cuerpo). En este apartado vamos a introducir el trabajo tal y como lo entendemos en Física, centrándonos sobre todo en un tipo de trabajo específico denominado trabajo mecánico.

Por otro lado, en apartados anteriores introdujimos el concepto de fuerza y el de desplazamiento. En este apartado supondremos un punto material que se desplaza en linea recta sobre el que actúa una fuerza constante.

Signo del Trabajo

Según el ángulo que forman la fuerza y el desplazamiento podemos distinguir los siguientes casos:

• ϕ > 90º : Trabajo positivo o trabajo motor (W>0). Por ejemplo, el trabajo realizado por un caballo que tira de un carruaje
• ϕ < 90º : Trabajo negativo o trabajo resistente (W<0). Por ejemplo la fuerza de rozamiento
• ϕ = 90º : Trabajo nulo (W=0). Por ejemplo, el trabajo realizado por tu fuerza peso cuando te desplazas en coche.

EJEMPLO 1:

¿Qué requiere más trabajo: subir un bulto de 420 N a una colina de 200 metros de altura, o un bulto de 210 N a una colina de 400 metros de altura? (no consideramos el ángulo de aplicación de la fuerza, que para ambos caso el mismo).

¿Por qué?

Apliquemos la fórmula simple:

T = F •  X (Trabajo =  fuerza por distancia)

Para el bulto 1

Para el bulto 2

Respuesta: Requieren el  mismo trabajo, que es igual a fuerza por distancia

EJEMPLO 2

Un remolcador ejerce una fuerza paralela y constante de 4.000 N sobre un barco y lo mueve una distancia de 15 m a través del puerto. ¿Qué trabajo realizó el remolcador?

Datos:

F = 4.000 N

X = 15 m

T = ?

Fórmula

T = F · X (Trabajo = Fuerza . distancia)

Entonces

T = 4.000 N x 15 m = 60.000 J

Ejemplos de potencia

• Potencia para mover una masa

Deseamos subir 100 kg de materiales de construcción al séptimo piso de un edificio en construcción, es decir, a unos 20 metros del suelo. Deseamos hacerlo empleando una grúa y en 4 segundos de tiempo, así que debemos averiguar la potencia necesaria de la misma.

Para utilizar la fórmula P = w/t, debemos calcular el trabajo realizado por la grúa primero.

Para eso utilizamos la fórmula W = F. d. cos a = 100 x 9,8 x 20 x 1 = 19.600 N. Entonces: P = 19.600 N / 4 s, o sea, que la potencia de la grúa habrá de ser de 4900 W.

• Potencia que disipa una resistencia

Debemos calcular la cantidad de potencia que disipa una resistencia eléctrica de 10 ohmios, cuando la atravesamos con una corriente de 10 amperios. Aplicamos en este caso la fórmula P = R x I², de la siguiente manera: P = 10 x 10², lo cual arroja como resultado una potencia disipada de 1000 watts.