Posición

May 27, 2017
Posición. En física, la posición de una partícula indica su localización en el espacio o en el espacio-tiempo. Se representa mediante sistemas de coordenadas.

En mecánica clásica, la posición de una partícula en el espacio se representa como una magnitud vectorial respecto a un sistema de coordenadas de referencia. En relatividad general, la posición no es representable mediante un vector euclidiano, ya que en el espacio-tiempo es curvo en esa teoría, por lo que la posición necesariamente debe representarse mediante un conjunto de coordenadas curvilíneas arbitrarias, que en general no pueden ser interpretadas como las componentes de un vector físico genuino. En mecánica cuántica, la representación de la posición de una partícula es aún más compleja, debido a los efectos de no localidad relacionados con el problema de la medida de la mecánica cuántica.

En general, en un sistema físico o de otro tipo, se utiliza el término posición para referirse al estado físico o situación distinguible que exhibe el sistema. Así es común hablar de la posición del sistema en un diagrama que ilustre variables de estado del sistema.

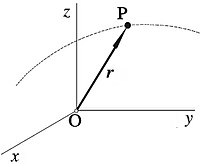
Posición de un punto P en un sistema de coordenadas cartesianas.

Vector posición en mecánica clásica

En mecánica clásica, debido al carácter euclídeo del espacio, la posición de una partícula se representa mediante el vector de posición o radio vector, usualmente simbolizado con la letra {\mathbf {r}} o mediante las coordenadas del punto geométrico del espacio en el que se encuentra la partícula.

La diferencia del vector posición entre dos posiciones distintas recibe el nombre de vector desplazamiento y se le designa por Δ r {\displaystyle \Delta \mathbf {r} \,} (desplazamiento finito) o por d r  {\displaystyle d\mathbf {r} \,} (desplazamiento infinitesimal).

{\displaystyle \mathbf {r} ={\mbox{OP}}=x\mathbf {i} +y\mathbf {j} +z\mathbf {k} \,}

Sistemas de referencia

Vector de posición de una partícula en el sistema de coordenadas cartesianas.

Podemos representar la posición de una partícula o de un punto del espacio, respecto de un sistema de ejes, mediante las coordenadas cartesianas (x,y,z) del punto, respecto al origen «O» del sistema de coordenadas (Figura 1). Dicho vector de posición se define como el vector que tiene como origen el punto «O» y como extremo el punto «P», es decir, el vector aplicado en el punto «O» que tiene como componentes las coordenadas cartesianas x, y, z, del punto «P». Escribiremos

  {\displaystyle \mathbf {r} ={\mbox{OP}}=x\mathbf {i} +y\mathbf {j} +z\mathbf {k} \,}

siendo i{\displaystyle \mathbf {i} ,\mathbf {j} ,\mathbf {k} \,} los versores asociados a los ejes coordenados respectivos. En general, un sistema de referencia queda definido por un origen y una base vectorial asociada. Si la base vectorial es ortogonal (i.e., si los tres versores que la definen son perpendiculares entre sí), el sistema de referencia también es ortogonal.

Traslación y rotación del sistema de referencia

Vectores de posición de una partícula en dos sistema de coordenadas cartesianas paralelos entre sí pero con distinto origen.

Componentes del vector de posición de una partícula en dos sistema de coordenadas cartesianas con distinto origen rotados entre sí.

Merece particular atención considerar el vector de posición cuando cambia por traslación el sistema de referencia, pues entonces cambia el vector de posición del punto P. Entre los vectores del punto P respecto a los sistemas de referencia de origen en O y en O′ existe la relación

  {\displaystyle \mathbf {r} ={\mbox{OO}}'+\mathbf {r} '\,}

y, consecuentemente, las componentes del vector no son invariantes en las traslaciones del sistema de referencia.

De mismo modo, las componentes del vector de posición no son invariantes en las rotaciones del sistema de referencia, transformando sus componentes mediante la correspondiente matriz de rotación.

Derivada temporal del vector 

Cuando la partícula permanece en reposo en el sistema de referencia, sus coordenadas no cambian en el transcurso del tiempo y su vector de posición será constante:

{\displaystyle \mathbf {r} =x\mathbf {i} +y\mathbf {j} +z\mathbf {k} }

Si la posición de una partícula puntual P cambia con el tiempo, en un instante dado se representa por:

{\displaystyle \mathbf {r} (t)=x(t)\mathbf {i} +y(t)\mathbf {j} +z(t)\mathbf {k} }

En un sistema de referencia fijo, la base coordenada para expresar la posición de vectores tiene la propiedad de permanecer fija, con lo cual el vector velocidad respecto a un sistema inercial puede obtenerse simplemente derivando las componentes del vector respecto al tiempo:

  {\displaystyle \mathbf {v} (t)={\frac {d\mathbf {r} (t)}{dt}}={\frac {dx(t)}{dt}}\mathbf {i} +{\frac {dy(t)}{dt}}\mathbf {j} +{\frac {dz(t)}{dt}}\mathbf {k} }

Esto contrasta con el caso de un sistema de referencia móvil, en los que aparecen términos adicionales asociados al movimiento del referencial.

Derivada del vector de posición en referenciales en rotación

Cuando el movimiento de la partícula se describe a un sistema de referencia móvil (x,y,z) en rotación con respecto de un referencial fijo (X,Y,Z) con el que comparte el mismo origen, el vector de posición será el mismo en ambos referenciales y vendrá expresado por:

r ( t ) = x ( t ) i ( t ) + y ( t ) j ( t ) + z ( t ) k ( t ) {\displaystyle \mathbf {r} (t)=x(t)\mathbf {i} (t)+y(t)\mathbf {j} (t)+z(t)\mathbf {k} (t)} {\displaystyle \mathbf {r} (t)=x(t)\mathbf {i} (t)+y(t)\mathbf {j} (t)+z(t)\mathbf {k} (t)}

en el referencial móvil (x,y,z). Puesto que los versores cartesianos (i,j,k)son función del tiempo, al derivar el vector posición con respecto al tiempo aparecerán términos relacionados se obtiene:

d{\displaystyle {\frac {d\mathbf {r} (t)}{dt}}=\left({\frac {dx}{dt}}\mathbf {i} +{\frac {dy}{dt}}\mathbf {j} +{\frac {dz}{dt}}\mathbf {k} \right)+{\boldsymbol {\omega }}\times \mathbf {r} }

 {\displaystyle {\boldsymbol {\omega }}\,} la velocidad angular asociada a la rotación del referencial móvil con respecto al referencial fijo.

En términos de la geometría diferencial los términos adicionales tienen que ver con la conexión asociada al sistema de coordenadas o referencia escogido:

  {\displaystyle {\begin{cases}{\cfrac {d\mathbf {i} (t)}{dt}}=\left(\Gamma _{j1}^{1}\mathbf {i} +\Gamma _{j1}^{2}\mathbf {j} +\Gamma _{j1}^{3}\mathbf {k} \right)v^{j}\\\\{\cfrac {d\mathbf {j} (t)}{dt}}=\left(\Gamma _{j2}^{1}\mathbf {i} +\Gamma _{j2}^{2}\mathbf {j} +\Gamma _{j2}^{3}\mathbf {k} \right)v^{j}\\\\{\cfrac {d\mathbf {k} (t)}{dt}}=\left(\Gamma _{j3}^{1}\mathbf {i} +\Gamma _{j3}^{2}\mathbf {j} +\Gamma _{j3}^{3}\mathbf {k} \right)v^{j}\end{cases}}}

Donde:

  {\displaystyle \Gamma _{ij}^{k}\,} son los símbolos de Christoffel que caracterizan la conexión.
  {\displaystyle v^{j}\,} son las componentes de la velocidad.

En mecánica relativista

En la teoría especial de la relatividad el espacio-tiempo de Minkowski tiene geometría pseudoeuclídea pero en lo esencial existe una biyección entre ese espacio y  {\displaystyle \scriptstyle \mathbb {R} ^{4}} por lo que puede definirse un cuadrivector posición análogo en muchos aspectos de la mecánica clásica:

  {\displaystyle \mathbf {X} =(X^{0},X^{1},X^{2},X^{3})=(ct,x,y,z)\,}

La derivada de este vector respecto al tiempo propio resulta ser la cuadrivelocidad que es el análogo relativista de la velocidad de la mecánica clásica:

  {\displaystyle \mathbf {U} ={\frac {d\mathbf {X} }{d\tau }}=(U^{0},U^{1},U^{2},U^{3})=\gamma (c,v_{x},v_{y},v_{z})\,}

Sin embargo en la teoría general de la relatividad las cosas se complican debido a que en ese contexto el espacio-tiempo generalmente es curvo. En ese caso no existe una biyección directa entre el espacio-tiempo y el espacio euclídeo tridimensional y por tanto no resulta posible describir la posición de un punto del espacio-tiempo mediante un vector euclídeo. Aunque como el espacio-tiempo cuatridimensional es localmente difeomorfo con el espacio euclídeo tridimensional, pueden emplearse coordenadas curvilíneas que tienen leyes de transformación tensorial similares a un cuadrivector, aunque las cuatro coordenadas de un punto no pueden ser identificadas con un cuadrivector.

En mecánica cuántica

En mecánica cuántica no-relativista para la mayoría de los sistemas no puede hablarse de la posición de una determinada partícula o incluso de su trayectoria. Esto es una consecuencia del principio de incertidumbre de Heisenberg. En esta teoría las coordenadas intervienen sólo como argumento de la función de onda que describe un sistema, pero en general esas coordenadas no designan la posición de ninguna partícula

Guardar

More from my site

Entradas Relacionadas