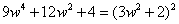Cuadrado de un binomio
Cuadrado de un binomio. El cuadrado de un binomio siempre es un trinomio. Sería de utilidad que memorice estos patrones para escribir cuadrados de binomios como trinomios. ( a + b ) 2 = a 2 + 2 ab + b 2. ( a – b ) 2 = a 2 – 2 ab + b 2. Ejemplos: Eleve al cuadrado cada binomio. a) ( x + 4) 2. ( x + 4) 2 = x 2+ 2( x · 4) + 4 2.
PRODUCTOS NOTABLES
En el estudio de la matemática, continuamente encontramos expresiones que mantienen la misma mecánica, son tan repetitivas que no necesitamos realizar la operación para conocer su respuesta, a este tipo de operaciones se les llama notables, y puede encontrarse su respuesta sin realizar la operación, lo que es lo mismo por simple inspección
Los productos notables son las multiplicaciones de tipo notable, en los capítulos presente y siguiente nos centraremos en los binomios potenciados, o sea los binomios elevados a alguna potencia.
Cuadrado de un binomio
Básicamente se escriben así:

Si efectuamos las operaciones nos queda:

Como se puede ver en ambos casos se sigue la misma mecánica y si se sustituye “a” o “b” o ambos por expresiones que incluyan tanto números como letras (25xy3z2) seguirán exactamente la misma mecánica. Se puede acortar como:

Que se leen respectivamente
- El cuadrado de la suma de dos cantidades ( (a + b)
 ) es igual al cuadrado de la primera (a
) es igual al cuadrado de la primera (a ) más el doble producto de ellas (2ab) más el cuadrado de la segunda (b
) más el doble producto de ellas (2ab) más el cuadrado de la segunda (b ).
).
- El cuadrado de la diferencia de dos cantidades ( (a – b)
 ) es igual al cuadrado de la primera (a
) es igual al cuadrado de la primera (a ) menos el doble producto de ellas (-2ab) más el cuadrado de la segunda (b
) menos el doble producto de ellas (-2ab) más el cuadrado de la segunda (b ).
).
Ejemplo:

Lo importante en los productos notables es que no es necesario operar solo aprender a reconocerlos y sustituirlos.
Cuadrado de un binomio
El cuadrado de un binomio siempre es un trinomio. Sería de utilidad que memorice estos patrones para escribir cuadrados de binomios como trinomios.
( a + b ) 2 = a 2 + 2 ab + b 2
( a – b ) 2 = a 2 – 2 ab + b 2
Ejemplos:
Eleve al cuadrado cada binomio.
a) ( x + 4) 2
( x + 4) 2 = x 2 + 2( x · 4) + 4 2
= x 2 + 8 x + 16
b) (2 y – 3) 2
(2 y – 3) 2 = (2 y ) 2 – 2(2 y · 3) + 3 2
= (2 y ) 2 – 2(6 y ) + 3 2
= 4 y 2 – 12 y + 9
c) (3 p – 2 q 2 )
(3 p – 2 q 2 ) = (3 p ) 2 – 2(3 p · 2 q 2 ) + (2 q 2 ) 2
= 9 p 2 – 2(6 pq 2 ) + 4 q 4
= 9 p 2 – 12 pq 2 + 4 q 4
Si los coeficientes de un trinomio ax 2 + bx + c satisficen la ecuación
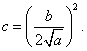
entonces el trinomio es el cuadrado perfecto del binomio
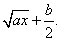
Ejemplo 1:
Factorice, si es posible.
x 2 – 14 x + 49
Aquí, a = 1, b = – 14, y c = 49. Tenemos:
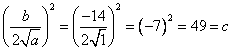
Así, el trinomio es un cuadrado perfecto:
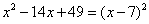
Puede verificar esto usando el FOIL .
Ejemplo 2:
Factorice, si es posible.
9 w 4 + 12 w 2 + 4
Aquí, a = 9, b = 12, y c = 4. (Podemos tratar a w 2 como x , y no preocuparnos por la cuarta potencia.)

Así, el trinomio es un cuadrado perfecto: